HUBUNGAN USAHA DAN ENERGI KELAS 10 IPA 3 dan 10 IPA 1

 Sekolah                                    : SMA AL AZHAR 3 B. LAMPUNG

Mata Pelajaran                        : Fisika

Kelas/Semester                        : X / Genap

Materi Pokok                           : Usaha (kerja) dan energi

Guru                                         : Rosmawati, S.Pd

Tujuan Pembelajaran

Setelah mengikuti proses pembelajaran, peserta didik diharapkan dapat:

·            1. Mengamati peragaan atau simulasi tentang kerja atau kerja

·          2. Mendiskusikan tentang energi kinetik, energi potensial (energi potensial gravitasi dan pegas),  hubungan kerja dengan perubahan energi kinetik dan energi potensial, serta penerapan hukum kekekalan energi mekanik

·         3.  Mendeskripsikan hubungan antara usaha, gaya, dan perpindahan.

·         4. Menghitung besar energi potensial (gravitasi dan pegas) dan energi kinetik.

·         5. Menganalisis hubungan antara usaha dan energi kinetik.

·        6.  Menganalisis hubungan antara usaha dengan energi potensial.

S        Sebelum ikut pelajaran Ibu,jangan lupa shalat dhuha

Hubungan Rumus Usaha dan Energi (Potensial dan Kinetik)

Usaha (W) merupakan gaya yang menyebabkan terjadinya perpindahan benda dari satu tempat ke tempat lainnya. Energi (E) adalah kemampuan untuk mengerjakan sesuatu dengan sifat kekal. Satuan usaha dan energi keduanya dinyatakan dalam satuan joule (j). Sifat energi tidak bisa dimusnahkan tetapi bisa berubah bentuk. Sebuah benda yang mengalami perubahan energi terjadi karena mendapatkan usaha dari gaya yang bekerja pada benda tersebut. Sehingga, antara usaha dan energi memiliki hubungan yang sangat erat. Hubungan tersebut dapat dinyatakan dalam sebuah hubungan rumus usaha dan energi.

Sebelumnya, ingat kembali bagaimana masing – masing nilai besar usaha dan energi diperoleh. Besar usaha (W) untuk memindahkan sebuah benda dengan gaya sebesar F sejauh s dinyatakan dalam rumus W = F × s. Besar energi tergantung dari jenis energi yang dialami suatu benda, misalnya pada energi potensial dan kinetik. Besar energi potensial (Ep) dipengaruhi oleh ketinggian (h) benda, sedangkan besar energi kinetik (Ek) dipengaruhi kecepatan (v) benda. Rumus mencari energi potensial dan energi kinetik berturut – turut dinyatakan dalam persamaan Ep = m · g · h dan Ek = 1/2 · m · V2·

Rumus usaha dan energi dapat dinyatakan dalam sebuah hubungan. Bagaimanakah hubungan rumus usaha dan energi potensial? Bagaimanakah hubungan rumus usaha dan energi kinetik? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Hubungan Usaha dan Energi Potensial

Besar energi potensial sangat dipengaruhi oleh ketinggian benda dari permukaan tanah. Semakin tinggi letak benda dari permukaan tanah, energi potensial yang ada pada benda tersebut semakin besar. Begitupula sebaliknya, semakin dekat/rendah letak benda dari permukaan tanah maka energi potensial benda tersebut semakin kecil. Selain ketinggian, besar energi potensial juga dipengaruhi oleh massa benda (m) dan gaya gravitasi (g) pada suatu tempat.

Perpindahan benda terjadi karena adanya usaha yang bekerja pada benda tersebut. Suatu benda yang terletak pada titik 1 dan bergerak ke titik 2 memerlukan usaha. Besarnya usaha gaya gravitasi sama dengan gaya gravitasi (m × g) dikalikan dengan perpindahan benda (h1 – h2).

Besarnya energi potensial gravitasi sama dengan energi potensial akhir dikurangi energi potensial mula – mula ( ΔEp = Epakhir – Epawal). Dengan ΔEp merupakan negatif perubahan energi potensial gravitasi. Persamaan ini menyatakan bahwa usaha yang dilakukan oleh gaya gravitasi sama dengan minus perubahan energi potensial gravitasi.

Baca Juga: Rumus Energi dan Daya Listrik

Hubungan Usaha dan Energi Kinetik

Setiap benda yang bergerak memiliki energi kinetik yang besarnya dipengaruhi oleh kecepatan benda. Besar energi kinetik akan semakin besar saat kecepatan yang dimiliki benda semakin tinggi, begitu juga sebaliknya. Energi dari benda bergerak timbul karena adanya usaha yang bekerja pada benda tersebut.

Sebelumnya, ingat kembali persamaan – persamaan pada Gerak Lurus Berubah Beraturan (GLBB). Besarnya kecepatan (V) dan jarak (s) yang ditempuh benda pada GLBB diberikan seperti persamaan berikut.

• Rumus kecepatan benda pada gerak lurus berubah beraturan:
  Vt = V0 · t + at
  Vt = 0 · t + at
  Vt = at

• Rumus jarak yang ditempuh benda pada gerak lurus berubah beraturan:
  s = V0 ·t + 1/2 · at2
  s = 0·t + 1/2 · at2
  s = 1/2 · at2
  at2 = 2s

Kedua persamaan di atas akan dibutuhkan pada penurunan rumus selanjutnya.  

Sebuah gaya (F) bekerja pada suatu benda dengan massa m yang berada pada titik 1 dengan kecepatan V1 = 0 (benda mula – mula dalam keadaan diam). Setelah t sekon, benda bergerak sejauh s dan berada pada titik 2 dengan kecepatan V2. Persamaan selisih kecepatan benda pada dua titik diberikan seperti berikut.

V22 – V12 = V22 – 02
V22 – V12 = (at)2
V22 – V12 = (at)2
V22 – V12 = a2 · t2
V22 – V12 = a · at2
V22 – V12 = a · 2s
V22 – V12 = 2as
as = 1/2(V22 – V12)

Persamaan selisih kuadrat kecepatan di atas akan berguna untuk menentukan rumus hubungan usaha dengan energi kinetik. Benda bergerak memerlukan usaha (W) yang besarnya tergantung pada besar energi kinetik benda. Hubungan usaha dan energi potensial terlihat seperti pada persamaan di bawah.

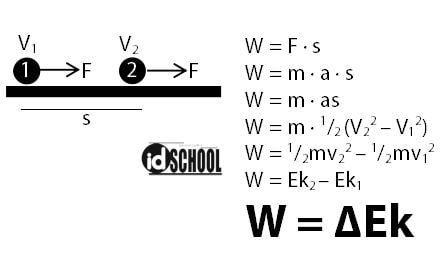
Baca Juga: Gerak Lurus Beraturan (GLB) dan Gerak Lurus Berubah Beraturan (GLBB)

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah akan menambah pemahaman sobat idschool terkait materi bahasan di atas. Setiap contoh soal dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan soal yang diberikan sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!

Contoh 1 – Soal Hubungan Usaha dan Energi Potensial

Sebuah benda dengan massa 4 kg jatug bebas dari ketinggian 15 m di atas tanah. Diketahui gaya berat benda pada saat mencapai tanah adalah 5 m dan besar gravitasi adalah 10 m/s2. Usaha yang telah dilakukan oleh benda tersebut sebesar ….
A. 200 joule
B. 400 joule
C. 600 joule
D. 800 joule
E. 1.000 joule

Pembahasan:

Berdasarkan informasi pada soal dapat diperoleh informasi seperti berikut.

• massa benda: m = 4 kg
• tinggi benda mula – mula: hA = 15 m
• tinggi benda pada ketinggian 5 m dari permukaan tanah: hB = 5 m
• gravitasi: g = 10 m/s2

Menghitung usaha:

WAB = –∆Ep
WAB = –(m·g·hB – m·g·hA)
WAB = –(4·10·5 – 4·10·15)
WAB = –(200 – 600)
WAB = –(–400)
WAB = 400 joule

Jadi, besar usaha yang dilakukan benda tersebut adalah sebesar 400 joule.

Jawaban: B

Contoh 2 – Soal Hubungan Usaha dan Energi Kinetik

Sebuah peluru dengan massa 4 gram ditembakkan pada pohon yang besar. Pada saat peluru menyentuh pohon, kecepatannya adalah 100 m/s. Gaya gesekan saat peluru menembus pohon dianggap tetap yaitu sebesar 100 N. Dalamnya lubang pada pohon yang tertembus oleh peluru adalah ….
A. 0,2 cm
B. 0,4 cm
C. 2 cm
D. 4 cm
E . 20 cm

Pembahasan:

Berdasarkan informasi yang diberikan pada soal dapat diperoleh informasi berikut.

• massa peluru: m = 4 gram = 4 × 10－3 kg
• Kecepatan peluru saat tepat mencapai pohon: v1 = 100 m/s
• Kecepatan peluru saat berhenti pada kedalaman batang pohon: v2 = 0 m/s
• Gaya gesek peluru dengan pohon: F = 100 N

Menghitung jarak/lubang pada pohon yang tertembus oleh peluru (s):

W = ∆Ek
F × s = Ek2 － Ek1
F × s = 1/2 · mv22 － 1/2 · mv12
F × s = 1/2 · m(v22 － v12)
100 × s = 1/2 · 4 × 10－3(1002 － 02)
100 × s = 2 × 10－3 × 104
100 × s = 2 × 10
100 × s = 20
s = 20/100 = 0,2 meter = 20 cm

Jadi, dalamnya lubang pada pohon yang tertembus oleh peluru adalah 20 cm.

Jawaban: E

TERIMAKASIH